Skip navigation

Research >> EIT Multiscale Optimization Framework

Computational Optimization Framework for Electrical Impedance Tomography (EIT)

Multilevel PCA-based Control Space Reduction

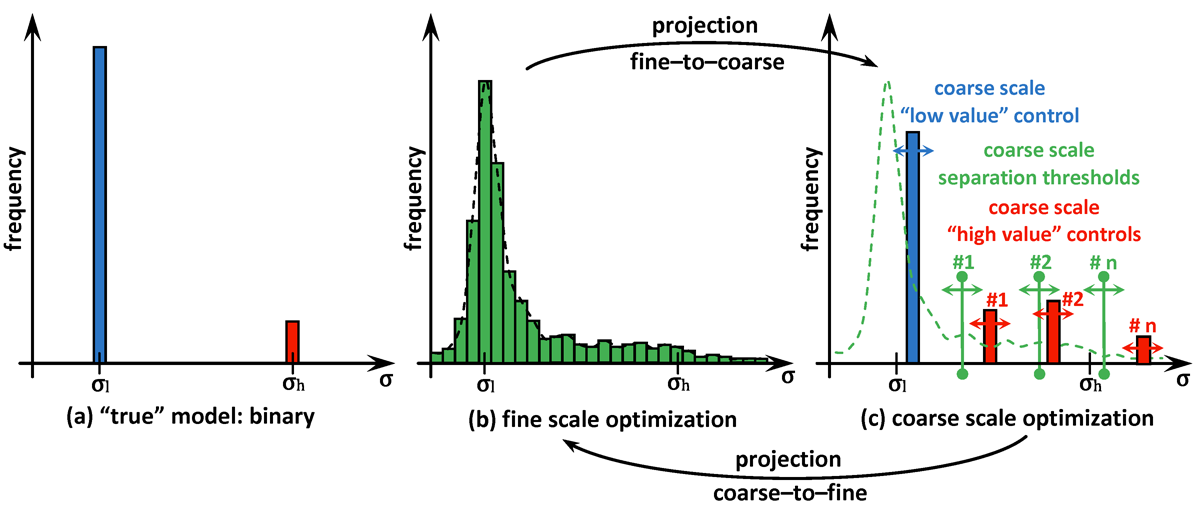
A novel computational approach for optimal reconstructing the physical properties of the media based on any available, possibly incomplete and noisy, measurements is created and validated. In particular, this approach is useful in various applications in biomedical sciences to operate with physical models characterized by near binary distributions observed for some of their physical properties, e.g. heat or electrical conductivity. The proposed computational framework is using gradient-based multiscale optimization techniques supplied with multilevel control space reduction over both fine and coarse scales used interchangeably. Proper "communication" established between scales in terms of projecting the solution from one scale onto another benefits in both quality and computational efficiency of the obtained results.

As seen in many practical applications, fine scale optimization performed on fine meshes is able to provide high resolution images for the searched distributions. Fine meshes also contribute enormously towards increased sensitivity by enforcing accuracy in computing adjoint states and constructing adjoint-based gradients if in use. The size of the control space defined over fine scales may be significantly decreased by applying any types of parameterization, for instance by using linear transformations based on available sample solutions (realizations) when applying principal component analysis (PCA). However, fine scale optimization may still suffer from over-parameterization if the problem is under-determined, i.e. the number of controls overweighs the size of available data (measurements). On the other hand, optimization performed on coarse meshes could arrive at a solution much faster due to the size of the control space. Usually, the solutions obtained at coarse meshes are of a low quality and less accurate due to sensitivity naturally "coarsened". In addition to this coarse scale optimization may suffer from being over-determined if the available data and the size of the control space are not properly balanced.

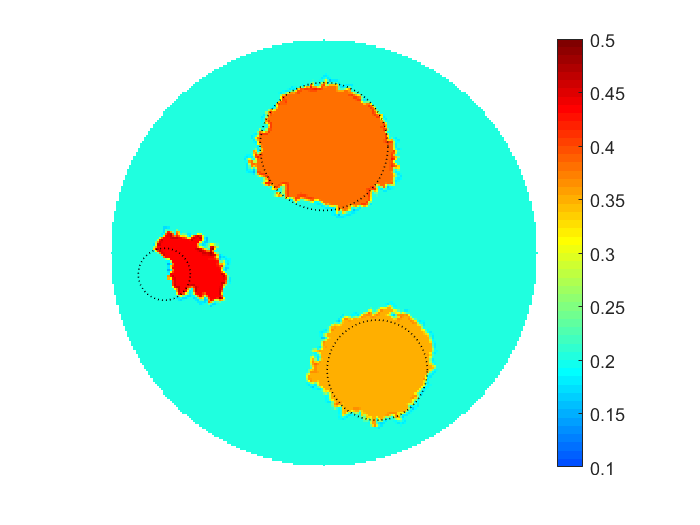
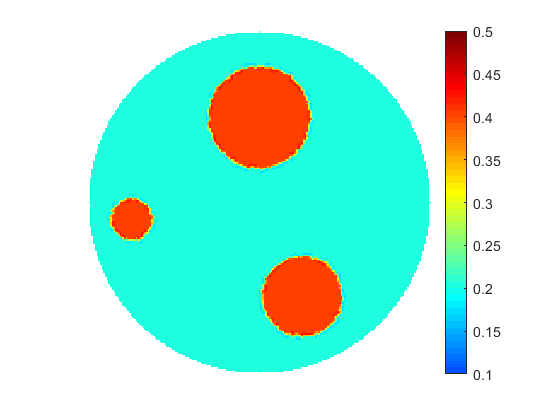
The proposed multiscale optimization framework utilizes all advantages mentioned above while using fine and coarse scales. Moreover, using them both in one process helps us mitigate their side effects. For example, fine scale solution images may not provide clear boundaries between regions identified by different physical properties in space. As a result, a smooth transition cannot provide an accurate recognition of shapes, e.g. of cancer-affected regions while solving an inverse problem of cancer detection (IPCD). In our computations, fine scale optimization is used to approximate the location of regions with high and low values of a physical parameter, namely electrical conductivity. Projecting solutions onto the coarse scale provides a dynamical (sharp-edge) filtering to the fine scale images optimized to better match the available data. The filtered images then projected back onto the fine scale preserving some information on recent changes obtained at the coarse scale. In fact, we developed a computationally efficient procedure for automated scale shifting in order to accumulate optimally progress obtained at both scales. In the current research, we keep the main focus on applying our new computational approach to IPCD by the Electrical Impedance Tomography (EIT) technique, however, this methodology could be easily extended to a broad range of problems in biomedical sciences, also in physics, geology, chemistry, etc.

Reconstruction of Biomedical Images by Efficient Sample-based Parameterization

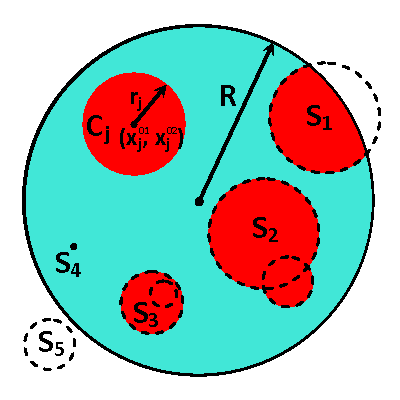
In this research, we develop a novel computational approach for optimal reconstruction of biomedical images based on any available measurements usually obtained with some noise. In particular, this approach is useful in various applications for medical practices dealing with models characterized by parameters with or near to binary-type distributions, e.g. heat or electrical conductivity. The proposed computational framework is built around a derivative-free optimization algorithm and supported by a set of sample solutions. These samples are generated synthetically with a geometry based on any available prior knowledge of the simulated phenomena and the expected structure of obtained images. The ease of parallelization allows operations on very large sample sets which enables the best approximations for the initial guess, and, as a result, close proximity to the local/global solution of the optimal control problem. The controls are effectively defined to utilize individual contributions from samples selected to represent the compound image and the efficient parameterization obtained from the description of the samples' geometry.

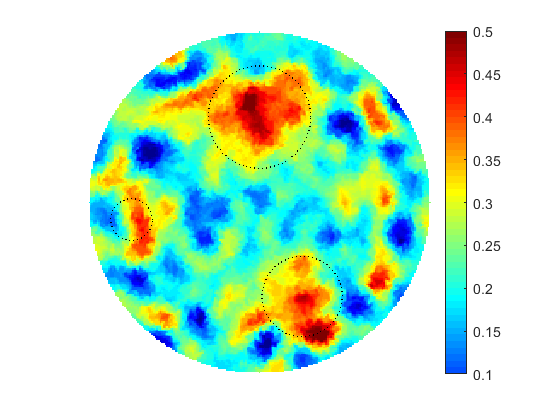
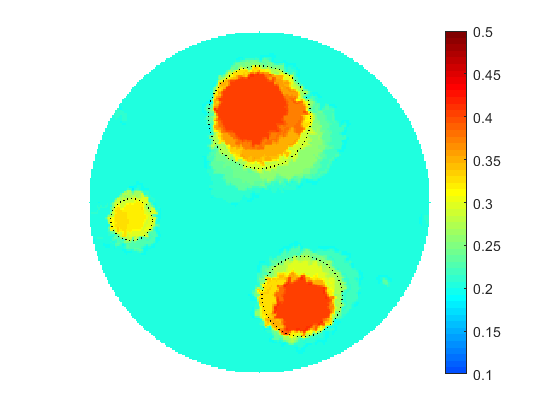
The proposed computational framework has an easy to follow design and is tuned by a nominal number of computational parameters making the approach simple for practical implementation for various applications also beyond biomedical imaging. High computational efficiency is achieved by applying the coordinate descent method customized to work with individual controls in the predefined custom order. We investigated the performance of the complete framework in applications to the 2D IPCD by the EIT technique. The proposed methodology of determining whether a certain region of the tissue contains a cancerous growth has superior efficiency in comparison with gradient-based techniques utilizing control space parameterization via PCA. This is due primarily to the predominately geometric nature of our approach, wherein we perturb known solutions to similar related problems in order to converge to the best available local/global minima.

Project Collaborators

References