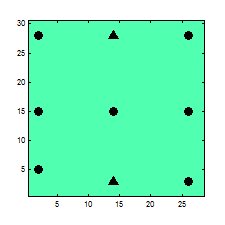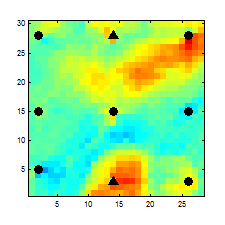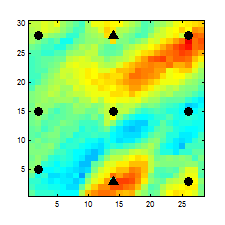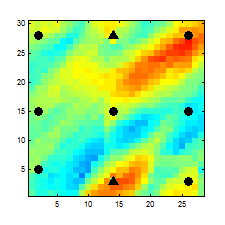
Reservoir production data, such as well phase rates and bottom-hole pressures (BHPs), are an important source of information that can be used to update the existing reservoir model and to reduce uncertainty in modeling the future reservoir behavior. History matching is a commonly employed name for this type of inverse problems of updating the reservoir model parameters to match the available measurements. Pursuing my current research goals I am developing a history matching algorithm which consists of detailed reservoir simulation, an adjoint gradient-based minimization of the production data mismatch with predictions, and some regularization techniques based on prior knowledge of main geological features of the reservoir structure.

Our computational framework addresses the main challenges arising in history matching for real field models, namely

• the complexity due to a large number of uncertain model parameters,
• presence of noise in the measurements, and
• deficit of the reservoir production data necessary for viable sensitivity information.

This framework utilizes Stanford's Automatic Differentiation-based General Purpose Research Simulator (AD-GPRS) to simulate the reservoir production and compute the adjoint field to obtain gradients of the objective function. This objective function includes the sum of square differences of production data mismatch and (if chosen) a regularization term, or the model mismatch term, which is assembled by means of employing analytic or sample covariance matrices.

Current and Future Work

History matching performed by the Optimization module in the AD-GPRS exhibits good results as it is utilizing the gradient which is computed very accurately by using a powerful automatic differentiation (AD) technique. However, very large number of optimization variables and shortage of the dynamic (production) data limit the potential of the gradient-based approach to small reservoir forecasting problems. My research is focusing on the following

• performing proper regularization techniques based on known geological and geostatistics features,
• adding geomechanics and seismic data,
• developing control space up-scaling performing proper space-scale parameterization,
• utilizing adjoint-based gradients for both history matching and production optimization via closed-loop reservoir modeling (CLRM),
• analysing Pareto optimal solutions for integrating production and time-lapse seismic data with noise of different levels, and
• developing novel mathematical concepts for building new models where relative permeability coefficients are approximated by multi-variable functions of fluid parameters.