Optimal Reconstruction of Constitutive Relations for Porous Media Flows
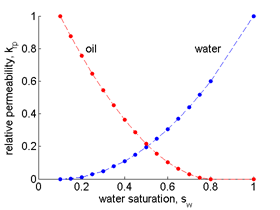
Mathematical models to represent the behavior of the underground fluids have been successfully used in the field of earth science engineering for years. Detailed description of the physical phenomena involved, efficiency, and accuracy of these models play crucial role in forecasting important industrial and economic parameters which influence the economy not only of the United States but also worldwide. Enhancing the quality of the mathematical models helps effectively develop and properly manage the existing petroleum reservoirs as well as new ones. The ecological component of such efforts is clearly seen as an ability to prevent man-triggered natural disasters, e.g. carbon leaks, fracking-induced seismicity, etc. This project aims to contribute to these advancements by designing an efficient computational framework to reconstruct the constitutive relations (model parameters) for complex fluids, or more specifically, state-dependent parameters of porous media.
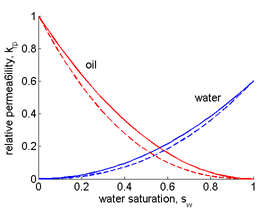
Comprehensive full-physics models for flow in porous media typically involve convection-diffusion partial differential equations (PDEs) whose parameters are unknown and have to be reconstructed from experimental data. Quite often these unknown parameters are coefficients represented by space-dependent, sometimes correlated, functions, e.g. porosity, permeability, transmissibility, etc. However, special complexity is seen when the reconstructed properties are considered as state-dependent parameters, e.g. the relative permeability coefficients. Modern petroleum reservoir simulators still use simplified approximations of such coefficients as single variable functions of phase saturation given in the form of tables or simple analytical expressions, e.g. Corey or LET models. This form is hardly reliable in modern engineering applications used, e.g., for enhanced oil recovery, carbon storage, modeling thermal and capillary pressure relations.
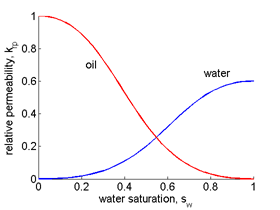
Thus, the main focus of the current project is on developing a novel mathematical concept for building new models where relative permeability coefficients are approximated by multi-variable functions of fluid parameters, namely phase saturations and temperature. Reconstruction of such complicated dependencies requires advanced mathematical and optimization tools to enhance the efficiency of existing engineering procedures with a new computational framework generalized for use in various earth science applications.
Project Collaborators
- Khalid Aziz (Stanford University)
- Louis J. Durlofsky (Stanford University)
- Oleg Volkov (Stanford University)
- Bartosz Protas (McMaster University)
