Efficient Control Space Parameterization
As seen in many practical applications, optimization performed on fine meshes is able to provide better solutions, e.g. high resolution images for the searched distributions. Fine meshes also contribute enormously towards increased sensitivity by enforcing accuracy in computing adjoint states and constructing adjoint-based gradients if in use.
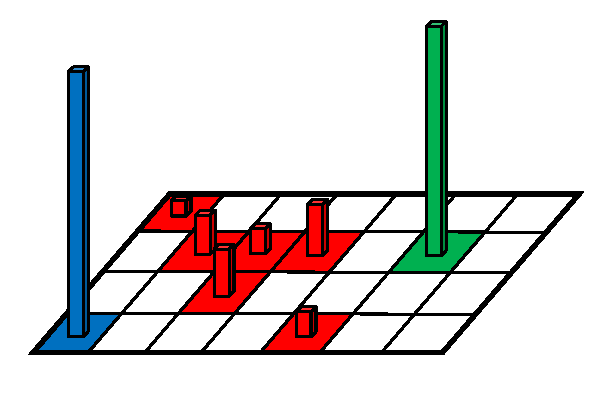
The size of the control space defined over fine scales may be significantly decreased by applying any types of parameterization, for instance by applying principal component analysis (PCA). However, fine scale optimization may still suffer from over-parameterization if the problem is under-determined, i.e. the number of controls overweighs the size of available data (measurements). On the other hand, optimization performed on coarse meshes could arrive at a solution much faster due to the size of the control space. Usually, the solutions obtained at coarse meshes are of a low quality and less accurate due to sensitivity naturally "coarsened". In addition to this coarse scale optimization may suffer from being over-determined if the available data and the size of the control space are not properly balanced.
In general, efficient parameterization is characterized by
- reasonably small number of parameters (controls) which implies fewer local minima,
- dynamical control space re-parameterization to follow changes in the solution and/or gradient structures,
- honoring any available prior information by limiting the space of feasible solutions,
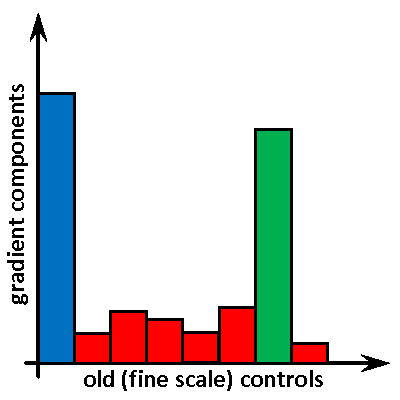
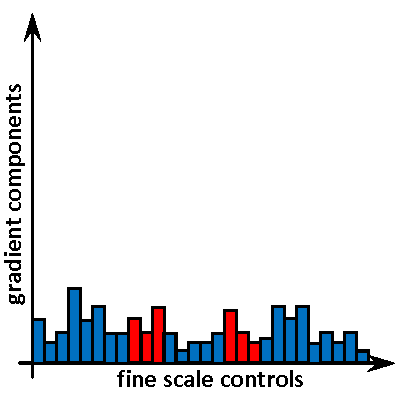
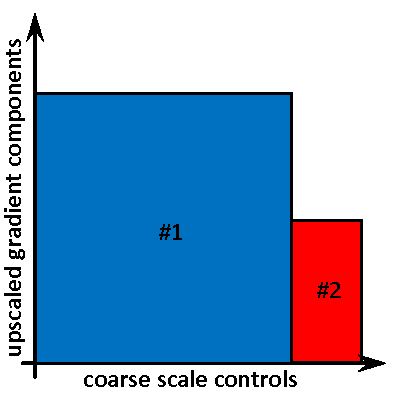
- preserving accuracy of gradients by computing their components on fine meshes, and
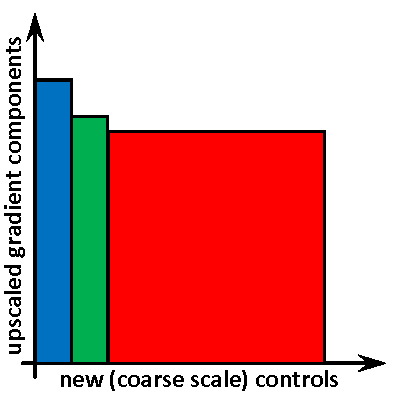
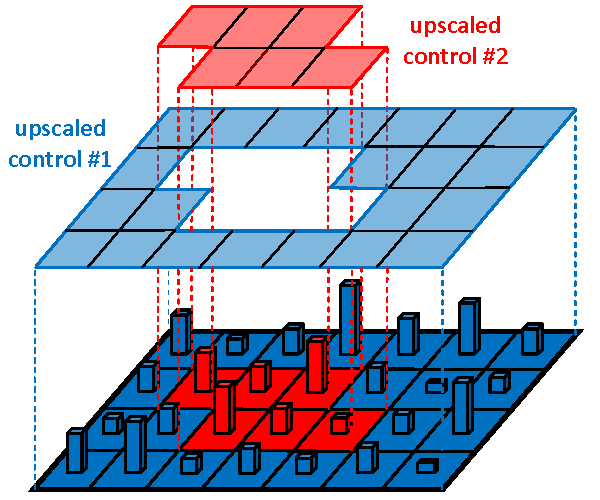
- applying proper techniques to transfer (project) gradients and obtained solutions between fine and coarse meshes to use benefits of both and maintain consistency with the solved problem.
Examples of efficient parameterization techniques
- principal component analysis (PCA),
- spatial grouping based on mesh structure,
- gradient-based grouping, e.g. GBME,
- multiscale optimization with multilevel control space reduction,
- sample-based parameterization.