Optimal Reconstruction of Material Properties in Complex Multiphysics Phenomena
PhD Dissertation, McMaster University, supervisor Prof. Bartosz Protas

In this study we investigated a novel computational approach to reconstruction of constitutive relations based on incomplete and noisy measurement data. This parameter estimation problem is solved using a gradient-based optimization technique in which the sensitivities of the cost functional with respect to the form of the constitutive relation are computed using a suitably-defined adjoint system. The main challenge inherent in this problem follows from the fact that the control variable is a function of the state, rather than the independent variable in the governing system. We studied the problem in the context of the "optimize-then-discretize" approach to PDE-constrained optimization and demonstrated how one can obtain an expression of the cost functional gradient. We also argued that the traditional L2 cost functional gradients are discontinuous, or do not have a required degree of regularity, and therefore are unsuitable for reconstruction of smooth constitutive relations. It was shown that this difficulty can be resolved by using the Sobolev gradients defined consistently with the functional setting of the problem in the optimization algorithm.
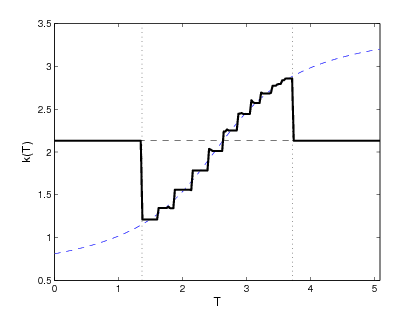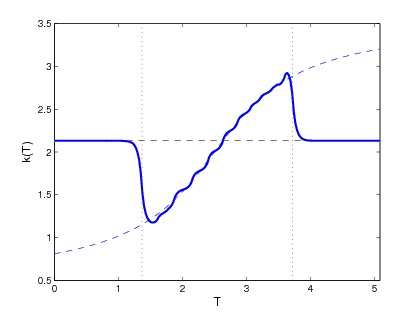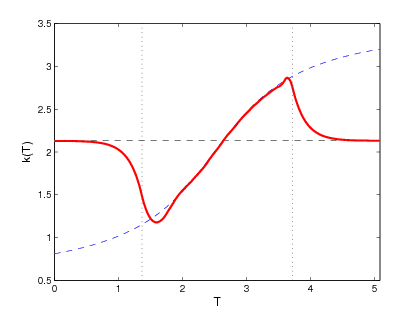
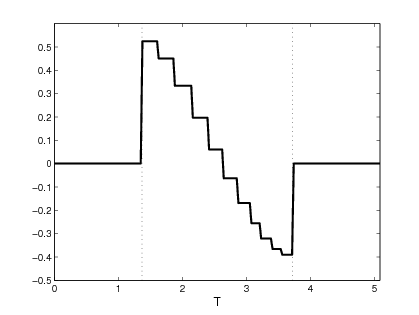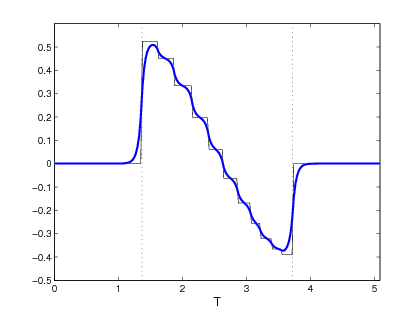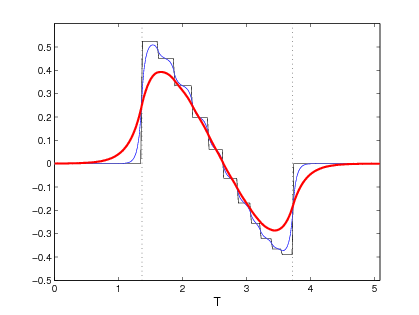
We also proposed and validated a procedure allowing one to shift, or extend, the identifiability region, and in this way reconstruct the constitutive relation over a much broader range of the state variable. A first set of computational tests demonstrated the feasibility of the proposed approach on a simple 1D model problem providing a proof of concept for the method. We then extended this approach to more complex multiphysics phenomena to demonstrate its applicability to time-dependent systems where the reconstructed property used in one conservation equation is a function of a state variable governed by a different conservation equation. We also addressed the important issue of reconstruction in the presence of random noise in the measurement data, and showed that the classical Tikhonov regularization is able to stabilize the reconstruction process. Our computations indicated that the use of suitable Sobolev gradients in the reconstruction process may also have some regularizing effect. We also addressed a number of computational challenges related to accurate and efficient evaluation of cost functional gradients, which are at a heart of the reconstruction procedure. As these gradients are given in terms of integrals over manifolds defined by a level-set function (in 2D and 3D), we analyze and compare three different methods for evaluation of cost functional gradients. We also demonstrate, both theoretically and computationally, the superior accuracy and efficiency of our novel numerical approach to the evaluation of these gradients.
Vorticity (left) and adjoint vorticity (right) fields evolving in time (2D lid-driven cavity flow)
Temperature (left) and adjoint temperature (right) fields evolving in time (2D lid-driven cavity flow)
References
- V. Bukshtynov, "Computational Methods for the Optimal Reconstruction of Material Properties in Complex Multiphysics Systems", Ph.D. Dissertation, McMaster University, Open Access Dissertations and Theses. Paper 6795. http://hdl.handle.net/11375/11859, 2012.
- V. Bukshtynov and B. Protas, "Optimal Reconstruction of Material Properties in Complex Multiphysics Phenomena", Journal of Computational Physics 242, 889-914, 2013 (the final version of the paper is available at doi: 10.1016/j.jcp.2013.02.034; see also arXiv:1301.5922).
- V. Bukshtynov, O. Volkov, and B. Protas, "On Optimal Reconstruction of Constitutive Relations", Physica D 240, 1228-1244, 2011 ([PDF file, 512 Kb], the final version of the paper is available at doi: 10.1016/j.physd.2011.04.006).
Examples of applications to other classes of problems
- I. Danaila, B. Protas, "Optimal reconstruction of inviscid vortices", Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 471(2180), 2015 (the final version of the paper is available at doi: 10.1098/rspa.2015.0323; see also arXiv:1411.7365).
- B. Protas, B. R. Noack, J. Osth, "Optimal Nonlinear Eddy Viscosity in Galerkin Models of Turbulent Flows", Journal of Fluid Mechanics 766, 337-367, 2015 (the final version of the paper is available at doi: 10.1017/jfm.2015.14; see also arXiv:1406.1912).
- A. K. Sethurajan, S. Krachkovskiy, I. C. Halalay, G. R. Goward and B. Protas, "Accurate Characterization of Ion Transport Properties in Binary Symmetric Electrolytes Using In-Situ NMR Imaging and Inverse Modeling", The Journal of Physical Chemistry - B 119, 12238-12248, 2015 (the final version of the paper is available at doi: 10.1021/acs.jpcb.5b04300).
- B. Protas, B. R. Noack, M. Morzynski, "An Optimal Model Identification for Oscillatory Dynamics with a Stable Limit Cycle", Journal of Nonlinear Science 24(2), 245-275, 2014 (the final version of the paper is available at doi: 10.1007/s00332-013-9188-z; see also arXiv:1209.4416).
The 2012 Cecil Graham Doctoral Dissertation Award
Canadian Applied and Industrial Mathematics Society (CAIMS)
Plenary Lecture at CAIMS 2013 Annual Meeting (Quebec City, Canada, June 2013) is available here [PDF file, 5.18Mb].
